前回の優しい経営学（ゲーム理論：ゲームセオリー）を書いたのは８月２０日だったのですね。　こりゃ、スゴイあいだが開いてしまいました。モウシワケアリマセン。

さて、今回からはすこしスタティステックス（統計学：statistics）に関して書いて行くつもりです。

最近の社会科学（ソーシャル サイエンス：social sciences）では統計学がないと何も出来ないと言い切れるかもしれません。例えば、俗に言うAI：人工知能（アーティフィシャル インテリジェンス：Artificial  intelligence）の根幹の理論とも言えます。

それと、これからは本エッセイではできるだけカタカナ（英語）を使用して行きます。スペルまで覚えることが出来れば100点ですが、せめて、カタカナで覚えることができれば・・・　

世界中の若者と言葉が通じるのです。

でもね、これ英語だと思わないで欲しいのです。「人工知能」と覚えずに「アーティフィシャル インテリジェント」と覚えれば良いのです。

年寄りに通じる言葉よりこれからの世界に通じる言葉を覚えるべきです。

そういう意味でカタカタの使用はとても良い傾向だと思います。この国がアジアと世界から取り残されない最低限の方法です。

さて、ディビエーション（偏差値：Deviation）に戻りましょう。（私は偏差値と言う言葉には良い思い出はありません。成績悪かったしなぁ・・）

下の表はある学校（高校でも大学でも何でもいいです）の国語と数学のテストの点数表です。国語のテストは30人が受験、数学は25人が受験していますので、それぞれのマスは30と25です。

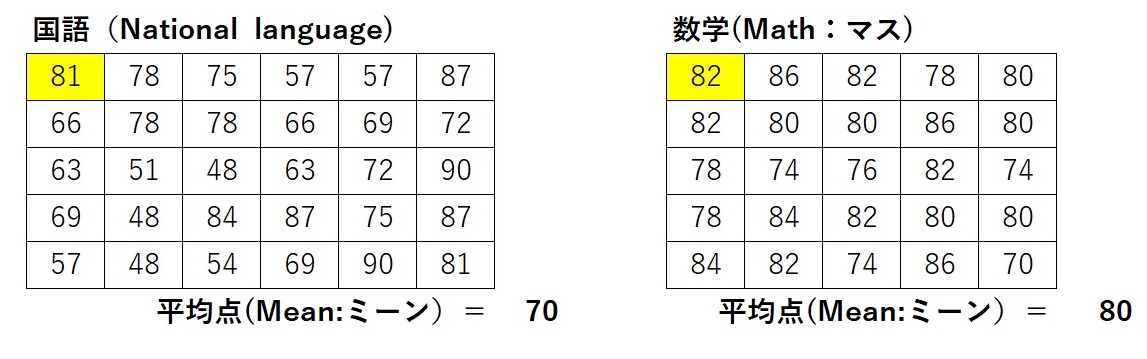
それぞれのミーン（平均点：Mean、統計学上ではアベレージではなく、このミーンを使います）は国語は70点、数学は80点です。

このクラスに転校してきたAさんが同じテストを受け、国語も数学も75点を取りました。

ここで問題です。Aさんの偏差値はいくらでしょうか？

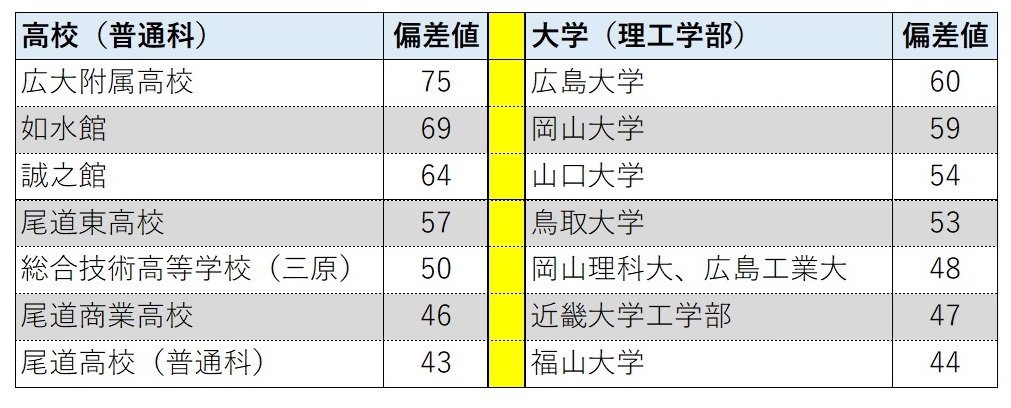
下の表は2020年版の近隣の高校と大学の偏差値を示しています。Aさんはどこなら入れるのでしょうか？

ますば、このテストの国語と数学それぞれの標準偏差（スタンダード ディビエーション：Standard Deviation）を計算します。

そのための方法としてはまず各自30人と25人の平均点からの差の二乗を求めます。国語と数学の最初のマスは81点と82点です（黄色のマス）。

国語　81（個人得点）-70（ミーン）= 11   →　11 × 11 = 121となります。

数学　82（個人得点）-80（ミーン）= 2    →　2 × 2 = 4となります。（黄色マス）

それぞれ、121と4が下記の表の最初のマスに入ります。同じように全てのマスを計算したものが下記の表です。

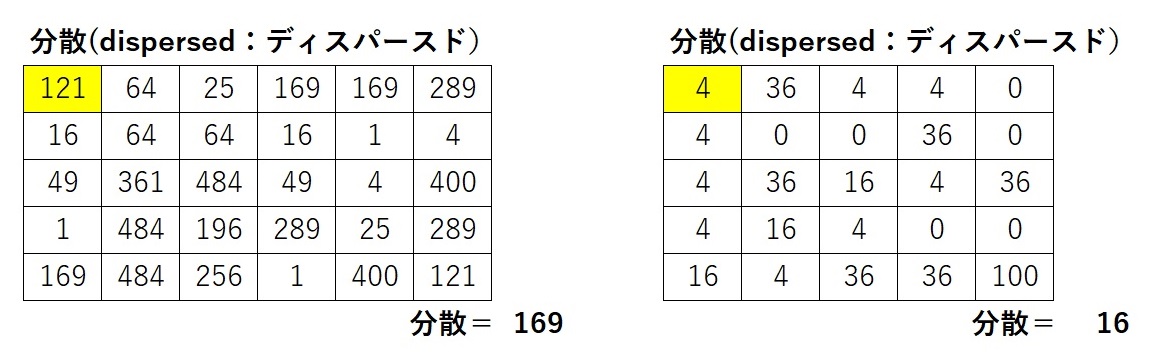
この計算値を全て合計しテストを受験した30人と25人でそれぞれ割ります。

 

国語の分散（ディスパースド：dispersed）は169、一方の数学のディスパースドは16です。

 

（数値の大小は点数のバラつきの大小を示してます。数学はみんなの点数が近いと言えます。また数値が小さい方が平均点に近いことを示します。）

 

この数値を√（ルート：平方根、正四角形の面積の求め方の逆）したものがスタンダード ディビエーション（標準偏差：Standard Deviation）と呼ばれるものとなります。　

169のルートは　12.99   (12.99×12.99=169)、

16のルートは4ですね。（4×4₌16）　　　なので、

国語のスタンダード ディビエーション（標準偏差）は12.99

数学のスタンダード ディビエーションは4

 

長々と書いていますが、中身はとても単純な内容ですので、のんびり読んでください。

 

で、転校生Aさんの偏差値です。Aさんの点は国語も数学も75点でした。上と同じ方法で計算すればよいのです。つまり。

国語　75(Aさんの点）- 70（ミーン） = 5　→　5 / 12.99(国語のスタンダード ディビエーション）₌ 0.38

数学　75(Aさんの点）- 80（ミーン）= -5   →　-5/4（数学のスタンダード ディビエーション）= -1.3

となります。　　　

 

え？　　普通の偏差値ってこんな数字じゃないで！！！

ですよね。

 

この国のディビエーションの表示方法は上記の0.38と-1.3をさらに加工した数値です。曰くこれらの数値に10を掛けて50を足す。とすると

国語　0.38×10＋50＝53.8               数学　-1.3×10＋50＝37　

 

お、なんだか身近な数値になりましたよね。なんでこんな計算するか？ですか？それはただ単純に身近な数値に置き換えるためです。なんの理屈も理論もありません。100が最大値になる様に計算式を作ったのでしょうね。（公式なんて所詮そんなもんです）

 

このディビエーション（偏差値）からAさんが入れる高校と大学を調べますと。

国語は入れる学校もあるが、数学はダメダメだぁ～～、もっと点取らなきゃ～！！　となります。

 

ちなみにこのディビエーション方式って、世界中でも使用しているのは日本と韓国だけ・・・・こう言うのが国際化（インターナショナル:International）を阻害している最大の原因かなぁ・・・と筆者は思っています。（でも、韓国の英語教育は凄いです。韓国の多くの若者は日本語より英語が話せます）

 

最近はどこの学校もAO（アドミッション オフィス:admissions office:主に大学の入学管理局）入学を取り入れ、独自の選択基準を持っているようですが、この方式もアメリカ方式とは微妙に異なる方法らしいですねぇ。